یک نیروی متناوب به یک سیستم یک درجه ازادی وارد می شه که از ما پاسخ سیستم رو می خواد.ابتدا با استفاده از برازش منحنی سری فوریه حاکم بر سیستم رو بدست می اوریم.سپس معادله رو تشکیل داده و با کمک دستور ode45 معادله رو حل می کنیم.

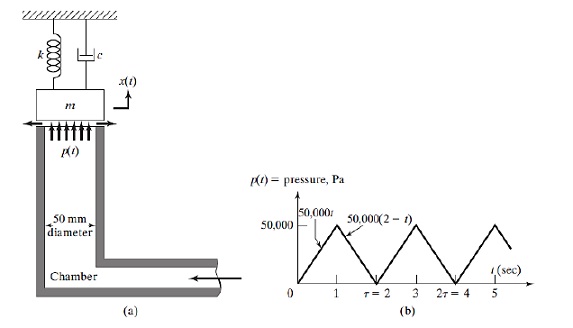
lکه در ان m=0.25 , k=2500 , c=10 می باشد.با ضرب مقدار فشار در سطح مقطع نیرو بدست میاد.پس برای زمانهای ۰تا۱ یک معادله ضرب در مساحت و در زمان ۱تا۲ هم یک معادله ضرب در مساحت می نویسیم و اون و تکرار می کنیم.سپس سری فوریه نیرو و محاسبه می کنیم. اسکریپت زیر معادله نیرو را رسم می کند.

t1=0:0.01:1;

y1=50000*t1*0.0020;

t2=1.01:0.01:2;

y2=50000*(2-t2)*0.0020;

t=0:0.01:6.02;

y=[y1 y2 y1 y2 y1 y2];

plot(t,y)

xlabel(‘time’)

ylabel(‘force’)

axis([0 6.02 0 100])

---

حالا با استفاده از برازش منحنی سری فوریه نیرو رو بدست میاریم.

---

fun=fit(t’,y’,'fourier5′)

fun = 

     General model Fourier5:

     per(x) = a0 + a1*cos(x*w) + b1*sin(x*w) + 

              a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w)+ 

              a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w)

     Coefficients (with 95% confidence bounds):

       a0 =       ۴۹٫۷۴  (۴۹٫۶۸, ۴۹٫۸۱)

       a1 =      -۴۰٫۷۳  (-۴۰٫۸۲, -۴۰٫۶۴)

       b1 =      ۰٫۷۰۷۸  (۰٫۵۳۱۴, ۰٫۸۸۴۲)

       a2 =    ۰٫۰۰۳۷۳۳  (-۰٫۰۸۵۵۱, ۰٫۰۹۲۹۷)

       b2 =  -۰٫۰۰۰۱۲۹۸  (-۰٫۰۸۹۳۱, ۰٫۰۸۹۰۵)

       a3 =       -۴٫۵۲  (-۴٫۶۰۹, -۴٫۴۳۱)

       b3 =      ۰٫۲۳۵۸  (۰٫۱۳۳۳, ۰٫۳۳۸۳)

       a4 =    ۰٫۰۰۳۷۲۸  (-۰٫۰۸۵۵۲, ۰٫۰۹۲۹۸)

       b4 =  -۰٫۰۰۰۲۵۹۶  (-۰٫۰۸۹۴۴, ۰٫۰۸۸۹۲)

       a5 =      -۱٫۶۲۳  (-۱٫۷۱۲, -۱٫۵۳۴)

       b5 =      ۰٫۱۴۱۴  (۰٫۰۴۷۲۶, ۰٫۲۳۵۵)

       w =       ۳٫۱۲۵  (۳٫۱۲۴, ۳٫۱۲۷)

---

تابع فیت شده رو در شکل زیر مشاهده می کنید.البته با اندکی خطا(به علت پدیده گیبس)

>> plot(t,y,’r');hold on;plot(fun,’b')

معادله سیستم هم که کاملا مشخصه.معادله مرتبه دو سیستم رو به دو معادله مرتبه اول تبدیل می کنیم.

(m)d²x/dt²+(c)dx/dt+(k)x=f(t)

x(t=0)=0

dx/dt(t=0)=0

به عنوان تغییر متغیر داریم:

dx₁/dt=x₂

و معادله اصلی به صورت مقابل باز نویسی میشود:

mdx₂/dt+cx₂+kx₁=f(t)

حالا معادله دیفرانسیل به صورت دو معادله مرتبه یک در خواهد امد:

dx₁/dt=x₂

(dx₂/dt=1/m(f(t)-cx₂-kx₁

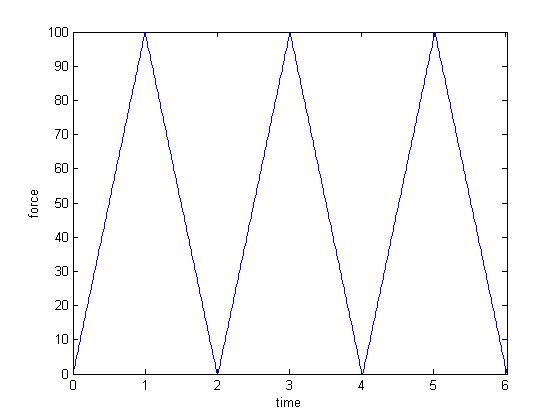
(f(t همان سری فوریه بدست امده می باشد.حالا نتایج رو در m.file ای ذخیره میکنیم.

---

function dx=fun(t,x)

dx=zeros(2,1);

a0 =49.74;

a1 =-40.73;

b1 =0.7078;

a2 =0.003733;

b2 =-0.0001298;

a3 =-4.52;

b3 =0.2358;

a4 =0.003728;

b4 =-0.0002596;

a5 =-1.623;

b5 =0.1414;

w =3.125;

m=0.25;

k=2500;

c=10;

dx(1)=x(2);

dx(2)=((1/m)*(a0 + a1*cos(t*w) + b1*sin(t*w) +… 

a2*cos(2*t*w) + b2*sin(2*t*w) + a3*cos(3*t*w) + b3*sin(3*t*w) +… 

a4*cos(4*t*w) + b4*sin(4*t*w) + a5*cos(5*t*w) + b5*sin(5*t*w)-c*x(2)-k*x(1)));

---

و حالا از تابع ode45 برای حل معادله سیستم استفاده می کنیم.

---

[t,x]=ode45(‘fun’,[0,6],[0,0]);

figure(1)

plot(t,x(:,1));

hold on

title(‘Time response of mechanical tranlation system’);

xlabel(‘Time – sec’);

---

.شاید دوست داشته باشین این سیستم رو با روش رانگ کوتا حل کنید و کدش رو بنویسید

---

a0 =49.74;

a1 =-40.73;

b1 =0.7078;

a2 =0.003733;

b2 =-0.0001298;

a3 =-4.52;

b3 =0.2358;

a4 =0.003728;

b4 =-0.0002596;

a5 =-1.623;

b5 =0.1414;

w =3.125;

m=0.25;

k=2500;

c=10;

dy1=@(t,y1,y2)y2;

dy2=@(t,y1,y2)(1/m)*(a0 + a1*cos(t*w) + b1*sin(t*w) +… 

a2*cos(2*t*w) + b2*sin(2*t*w) + a3*cos(3*t*w) + b3*sin(3*t*w) +… 

a4*cos(4*t*w) + b4*sin(4*t*w) + a5*cos(5*t*w) + b5*sin(5*t*w)-c*y2-k*y1);

h=.01;

t=0:h:10;

y1=zeros(1,length(t));

y2=zeros(1,length(t));

y1(1)=0;

y2(1)=0;

N=length(t);

for i=1:N-1

    k1 = dy1(t(i),y1(i),y2(i));

    m1 = dy2(t(i),y1(i),y2(i));

    k2 = dy1(t(i)+h/2,y1(i)+0.5*k1*h,y2(i)+0.5*m1*h);

    m2 = dy2(t(i)+h/2,y1(i)+0.5*k1*h,y2(i)+0.5*m1*h);

    k3 = dy1(t(i)+h/2,y1(i)+0.5*k1*h,y2(i)+0.5*m2*h);

    m3 = dy2(t(i)+h/2,y1(i)+0.5*k1*h,y2(i)+0.5*m2*h);

    k4 = dy1(t(i)+h,y1(i)*k3*h,y2(i)*m3*h);

    m4 = dy2(t(i)+h,y1(i)*k3*h,y2(i)*m3*h);

    

    y1(i+1) = y1(i) + (h/6)*(k1 + 2*k2 + 2*k3 +k4);

    y2(i+1) = y2(i) + (h/6)*(m1 + 2*m2 + 2*m3 +m4);

end

subplot(211)

plot(t,y1,’r')

grid

ylabel(‘displacement’)

xlabel(‘time’)

subplot(212)

plot(t,y2,’b')

grid

ylabel(‘velocity’)

xlabel(‘time’)

---

خوب پاسخ سیستم رو به صورت یکسری نقاط در اختیار داریم.برای بدست اوردن تابع سیستم دوباره از برازش منحنی استفاده می کنیم:

>> fit(t,x(:,1),’fourier5′)

ans = 

     General model Fourier5:

     ans(x) = a0 + a1*cos(x*w) + b1*sin(x*w) + 

              a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w)+ 

              a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w)

     Coefficients (with 95% confidence bounds):

       a0 =     ۰٫۰۱۹۸۹  (۰٫۰۱۹۸۸, ۰٫۰۱۹۸۹)

       a1 =    -۰٫۰۱۶۳۳  (-۰٫۰۱۶۳۴, -۰٫۰۱۶۳۲)

       b1 =  ۸٫۹۶۸e-005  (۷٫۰۰۶e-005, 0.0001093)

       a2 = -1.655e-005  (-۲٫۵۹۹e-005, -7.109e-006)

       b2 =  ۸٫۷۹۷e-007  (-۹٫۱۴۷e-006, 1.091e-005)

       a3 =   -۰٫۰۰۱۸۴۳  (-۰٫۰۰۱۸۵۲, -۰٫۰۰۱۸۳۳)

       b3 =  ۳٫۰۸۲e-005  (۱٫۹۴۸e-005, 4.216e-005)

       a4 = -1.808e-005  (-۲٫۷۶۱e-005, -8.546e-006)

       b4 =  ۲٫۰۱۶e-006  (-۷٫۷۹۳e-006, 1.183e-005)

       a5 =  -۰٫۰۰۰۶۸۵۸  (-۰٫۰۰۰۶۹۵۴, -۰٫۰۰۰۶۷۶۲)

       b5 =  ۱٫۹۹۱e-005  (۹٫۵۸۵e-006, 3.023e-005)

       w =       ۳٫۱۲۵  (۳٫۱۲۴, ۳٫۱۲۵)

 >>plot(ans)

مشاهده می کنید که نیرو و جابجایی سیستم از یک جنس می باشند.

---

اگر شما این مثال رو به روش تحلیلی حل کنید و بکمک متلب اون رو رسم کنید به شکل زیر می رسید.

.دوستان عزیز مشکلی بود تو نظرات با ما در نظرات در میان بزارید

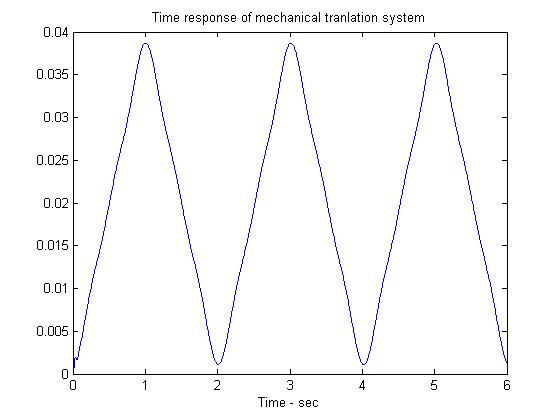
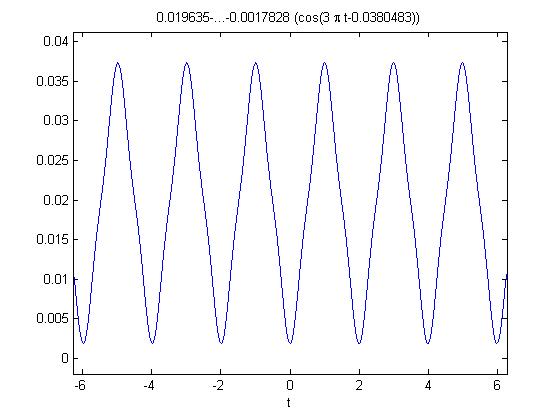
مسعود شمس

پاسخ سیستم یک درجه ازادی به برانگیزش کلی,ارتعاشات درمتلب,پاسخ واداشته سیستم با یک درجه ازادی,پاسخ یک سیستم یک درجه ازادی به برانگیزش کلی,پروژه ارتعاشات,پروژه ارتعاشات توسط متلب,پروژه ارتعاشات متلب,پروژه انجام شده ارتعاشات,Mathworks Matlab R2011b v7.13 Build 564٬ Mathworks Matlab R2012a٬ Mathworks Matlab R2012b٬ Mathworks Matlab R2012b 8.00 Build 783٬ آخرین ورژن Matlab٬ برنامه Matlab٬ جدیدترین ورژن Matlab٬ دانلود Mathworks MATLAB R2011b v7.13 Build 564٬ دانلود Mathworks Matlab R2012a٬ دانلود Mathworks Matlab R2012b٬ دانلود Mathworks Matlab R2012b 8.00 Build 783٬ دانلود MATLAB٬ دانلود برنامه Matlab٬ دانلود نرم افزار Matlab٬ سریال Matlab٬ فعال ساز Matlab٬ نرم افزار Matlab٬ پچ Matlab٬ کرک Matlab

امروز قراره معادلات گرمایی در فضای تک بعد رو با چند مثال بررسی کنیم.

برای حل معادله گرما در زمان t و در فضای تک بعدی از دستور pdepe استفاده می کنیم.

فرم کلی معادله سھمی وار متلب بصورت زیر می باشد.

و ھمین طور فرم کلی شرایط مرزی بصورت زیر می باشد.

که x_l نمایانگر نقطه ابتدا و x_r نمایانگر نقطه انتهایی شرایط مرزی می باشد.توجه کنید که b دارای مقدار ثابت در هر دو معادله است.هر کدام از معادله های بالا را در m.file جداگانه قرار می دهیم.مقادیر s,b,c را از مقایسه معادله حاکم در مثال با فرم کلی معادله سهمیگون در متلب بدست اورده و در m.file قرار می دهیم.مقادیر p,q را نیز از مقایسه شرایط مرزی مسئله با فرم کلی شرایط مرزی تعریف شده برای متلب بدست می اوریم.و در اخر نیز شرایط کرانه ای را در m.file سوم قرار می دهیم.سپس به کمک دستور pdepe سه m.file را ترکیب کرده معادله را حل می کنیم.

:Example

معادله  اصلی بصورت:

شرایط مرزی بصورت:

 

  

و شرایط اولیه بصورت:

کاملا مشخص است که مقدار c=1 می باشد.همچنین ما در طرف راست معادله حاکم بر مسئله مشتق دوم بر حسب x را داریم.پس مقدار b باید برابر u_x باشد.مقدار s نیز که به وضوح مشخص است که برابر ۰ می باشد. ملاحضه کردید که مقادیر c,b,s طوری در معادله سهمیگون مقدار دهی شدند که به معادله حاکم بر مسئله برسیم.مقدار m نیز باید برابر ۰ باشد تا عملا x از معادله حذف شود. m را در اخر مقدار دهی میکنیم.

کد زیر نمایانگر معادله اصلی و در eqn1.m ذخیره می کنیم.

---

function [c,b,s] = eqn1(x,t,u,DuDx)

%EQN1: MATLAB function M-file that specifies

%a PDE in time and one space dimension.

c = 1;

b = DuDx;

s = 0;

---

---

function value = initial1(x)

%INITIAL1: MATLAB function M-le that species the initial condition

%for a PDE in time and one space dimension.

value = 2*x/(1+x^2);

---

و حالا نوبت به حل مساله به کمک دستور pdepe رسیده است.مساله را در زمان ۱۰ثانیه نخست و طول واحد(مثلا یک لوله به طول واحد) حل می کنیم.

---

%PDE1: MATLAB script M-file that solves and plots

%solutions to the PDE stored in eqn1.m

m = 0;

% NOTE: m=0 specifies no symmetry in the problem. Taking

% m=1 specifies cylindrical symmetry, while m=2 specifies

% spherical symmetry.

%

% Define the solution mesh

x = linspace(0,1,20);

t = linspace(0,10,10);

%Solve the PDE

u = pdepe(m,@eqn1,@initial1,@bc1,x,t);

% Plot solution

figure(1)

surf(x,t,u);

title(‘Surface plot of solution’);

xlabel(‘Distance x’);

ylabel(‘Time t’);

figure(2)

for i=1:length(t)

   plot(x,u(i,:))

   hold on

end

---

جواب u بصورت یک ماتریس به اندازه t و x ذخیره شده است.برای مثال (u(1,5 مقدار دما در نقطه((t(1),x(5)

مشخص می کند.

ما می تونیم به کمک دستور((:,plot(x,u(1 بردار دما را در اغاز (t=0) رسم می کنیم.

:Example

وکد زیر رو برای مساله به این صورت می نویسیم:

مسعود شمس

اموزش متلب, pdepe, حل عددی معادله حرارت پاره ای وابسته به زمان, معادله حرارت در متلب, حل معادله حرارت در متلب,معادلات با مشتقات جزیی,معادلات با مشتقات جزیی در متلب,حل معادلات با مشتقات جزیی در متلب,پاسخ سیستم یک درجه ازادی به برانگیزش کلی,ارتعاشات درمتلب,پاسخ واداشته سیستم با یک درجه ازادی,پاسخ یک سیستم یک درجه ازادی به برانگیزش کلی,پروژه ارتعاشات,پروژه ارتعاشات توسط متلب,پروژه ارتعاشات متلب,پروژه انجام شده ارتعاشات,Mathworks Matlab R2011b v7.13 Build 564٬ Mathworks Matlab R2012a٬ Mathworks Matlab R2012b٬ Mathworks Matlab R2012b 8.00 Build 783٬ آخرین ورژن Matlab٬ برنامه Matlab٬ جدیدترین ورژن Matlab٬ دانلود Mathworks MATLAB R2011b v7.13 Build 564٬ دانلود Mathworks Matlab R2012a٬ دانلود Mathworks Matlab R2012b٬ دانلود Mathworks Matlab R2012b 8.00 Build 783٬ دانلود MATLAB٬ دانلود برنامه Matlab٬ دانلود نرم افزار Matlab٬ سریال Matlab٬ فعال ساز

منبع:http://www.icivil.ir/omran/civil-software/civil-software-learning/post-236.php

تحليل تير سراسري با استفاده از نرم افزار MATLAB

این برنامه به مانند یک ذره بین بر روی نمودارهای رسم شده عمل می نماید. کافیست فایل 'magnify.m' را پس از رسم نمودار مورد نظر اجرا نمود. با دکمه چپ ماوس بر روی نمودار یک پنجره بزرگنمایی شده ظاهر می گردد. از کلیدهای '>' یا '<' برای بزرگ و کوچک کردن پنجره و از کلیدهای '+' و '-' نیز می توان برای بزرگنمایی جزئیات درون پنجره استفاده نمود. در نهایت با دکمه سمت راست یا کلید 'Ctrl' می توان پنجره جدید را ثابت نمود. 

این فایل از نمونه برنامه هایی می باشد که در سایت http://www.mathworks.ch/matlabcentral/ توسط کاربران نوشته شده و به اشتراک گذاشته شده است. در صورت علاقه نمونه های مفیدی از این نوع برنامه ها همراه با کد آنها در این سایت به اشتراک گذاشته شده است. 

پس از دانلود m-فایل برنامه آدرس فعال matlab را به پوشه آن تغییر داده و پس از اجرای کد زیر بر روی نمودار ایجاد شده کلیک کنید!

MATLAB زبانی است که کاربرد کامپیوتر در مهندسی را با کارائی بالا تضمین کرده و امکانات محاسباتی، تصویری، و برنامه نویسی را در محیطی آسان و آشنا فراهم میکند. کارائی MATLAB در مقوله هائی نظیر: محاسبات ریاضی، آنالیز داده ها، مدل سازی و شبیه سازی، گرافیک، و تولید نرم افزار (حتی برای محیط ویندوز) به اثبات رسیده است.
این زبان با توجه به نظرات کاربران دانشگاهی و صنعتی دستخوش بازنگری های زیادی شده و اکنون به زبان استاندارد جهت آموزش های مقدماتی و عالی و ابزار پژوهش و توسعه در صنایع تبدیل شده است.
MATLAB جعبه ابزارهائی برای کاربردهای خاص در اختیار قرار می دهد، که از جمله آنها جعبه ابزار ریاضیات، کنترل، شبکه های عصبی، بازرگانی و . . . می باشند. جعبه ابزارها با زبان متلب و به صورت مجموعه هایی از ام- فایل ها گسترش یافته اند و برای هر کاربر در زمینه تخصصی اش کاربرد و اهمیت زیاد دارند. امکان ساخت جعبه ابزارهای جدید و شخصی نیز برای کاربران پیشرفته فراهم است. متلب دارای پنج ویژگی شایان ذکر است:

• پنجره ی واسط کاربر IDE) Integrated Development Environment) بسیار دلپذیر و دست یافتنی که از امتیازات برنامه نویسی متنی و گرافیکی در کنار هم استفاده می کند. این واسط کاربر شامل پنجره های: فرمان، دایرکتوری جاری، تاریخچه فرمان، فضای کار و . . . است. پنجره ی فرمان ، دستورات را به صورت کنسول یا خط فرمان، مشابه برنامه نویسی DOS دریافت و اجرا می کند. پنجره فضای کار کلیه متغیرهای فضای کار را با مشخصات آنها نمایش می دهد. پنجره های واسط کاربر دینامیک بوده و ممکن است خود شامل پنجره های فرعی باشند. همیشه با اجرای زیرمنوی Default از منوی اصلی می توان چهار پنجره ی Command, Command History, Workspace, Current Directory را که کاربردی تر هستند، ظاهر کرد و در دسترس داشت.

• کتابخانه ی عظیمی از توابع مقدماتی و پیشرفته

• زبان قوی هم برای فرامین کوتاه و یکبار مصرف و هم برای برنامه نویسی بزرگ و کاربردی

• روش های متعدد ترسیمات دو بعدی و سه بعدی

• واسط میان برنامه ای Application Program Interface-API که امکان فراخوانی برنامه های متلب از زبان های Fortran و C تبدیل فایل های متلب (ام- فایلها) به زبان C استفاده از موتور محاسباتی متلب در این زبانها را فراهم می کند. با اسفاده از تبدیلات فوق می توان برنامه های نوشته شده در محیط متلب را به صورت اجرائیِ کنسولی (قابل اجرا از خط فرمان سیستم عامل) درآورد. همچنین امکان تهیه فایلهای اجرائی با واسط گرافیکی برای ویندوز وجود دارد.

شایان ذکر است پیش تر کاملترین مجموعه فیلم های آموزشی نرم افزار مهندسی Matlab در تمامی علوم و شاخه ها را خدمتتان معرفی کردیم که با استقبال بسیار زیاد دوستان رو به رو گشت، بدین منظور بر آن شدیم تا مجموعه جامع فیلم ها آموزشی Matlab به زبان فارسی را بنا به در خواست دوستان و اهمیت این نرم افزار، برای اولین بار از طریق مهندس یار خدمتتان ارائه کنیم. شاید به جرائت بتوان گفت این مجموعه از پایه ترین مباحث تا پیشرفته ترین مباحث را در خود جای داده است. از ویژگی های بارز این مجموعه می توان به سادگی بیان، مثال های متعدد و کاربردی جهت یادگیری نام برد. این مجموعه در دو قسمت مجزا خدمت شما دوستان عزیز ارائه می گردد.

قسمت اول :

• مقدمه
• آموزش نصب برنامه
• آشنایی با محیط نرم افزار
• آشنایی با پنجره Command
• آشنایی با پنجره Command History
• آشنایی با پنجره Varible Editor
• تعریف کردن متغیر و ماتریس
• آدرس دهی در ماتریس ها
• عملگر ها در Matlab
• انجام چهار عمل اصلی بر روی ماتریس ها
• قواعد تعریف متغیر در Matlab
• انجام اعمال اصلی به صورت درایه به درایه
• به کار بردن عملگر های شرطی
• پارامتر های اولیه
• آشنایی با دستور Disp
• آشنایی با دستور Input
• آشنایی با آرایه های خاص
• برخی از دستورات پر کاربرد در جبر ماتریسی
• آشنایی با m-file
• آشنایی با function
• بدست آوردن میانگین

قسمت دوم:

• نحوه استفاده از دستور if
• نحوه استفاده از دستور switch
• نحوه استفاده از دستور for
• استفاده از عملگر های منطقی در شرط
• استفاده از تابع formt
• نوشتن توابع چند جمله ای در Matlab
• بدست آوردن ریشه یک چند جمله ای ها
• بدست آوردن مقدار یک چند جمله ای ها
• محاسبه ضرب و تقسیم در چند جمله ای ها
• محاسبه مشتق در چند جمله ای ها
• محاسبه انتگرال در چند جمله ای ها
• ایجاد توابع چند متغیره
• مقدار دهی به توابع چند متغیره
• محاسبه مشتق در توابع چند متغیره
• محاسبه انتگرال در توابع چند متغیره
• نحوه محاسبه ماتریس ژاکوبین
• ترسیم توابع دو بعدی
• ترسیم توابع سه بعدی

  دانلود مستقیم : بخش اول  |   بخش دوم

  حجم فايل : 700 مگابایت 

  پسورد فايل : www.mohandesyar.com 

 لینک منبع

دانلود برنامه متلب conformal

برای دانلود اینجا کلیک کنید...

http://www.4shared.com/file/xxn4Q9lf/conformal2.html

Remote Sensing Digital Image Analysis

John A. Richards · Xiuping Jia

Remote_Sensing_Digital_Image_Analysis_Richard_2006.pdf

برای دانلود اینجا کلیک کنید...

http://www.4shared.com/office/3JoHHi2Y/Remote_Sensing_Digital_Image_A.html

کد های Matlab برای تحلیل المان محدود سازه

نوشته: A.J.M. Ferreira, Springer

تعداد صفحات: 236

حجم فایل: 3.838 مگابایت

نوع فایل: pdf

لینک مستقیم دانلود

گزیده ای از مطالب:

• مقدمه ای کوتاه بر معرفی نرم افزار Matlab {توابع اسکالر برداری و ماتریسی - گرافیک - جبر خطی}
• سیستم های گسسته {فنر - میله Bar - تعادل node ها}
• تحلیل میله Bar و کدنویسی آن
• آنالیز خرپای 2 و 3 بُعدی
• آنالیز تیر اویلر- برنولی
• آنالیز قاب (فریم) دو و سه بعدی
• آنالیز تیر تیموشنکو
• Plane stress
• آنالیز صفحات Mindlin
• آنالیز Laminated plates

کتاب خوبیه برای کسانی که می خواند با نرم افزار Matlab به صورت تخصصی در زمینه المان محدود(FEM) کار کنند.

موفق و سر بلند باشید

کد به صورت تابع نوشته شده است. ماتریس مورد نظر را به تابع داده و یک ماتریس با یک ردیف که به صورت زگزاگی اسکن شده است می دهد.

حتما ماتریس باید ۸ در ۸ باشد.

function row=zigzagscan(matrix)

ss=1;

ii=1;

jj=1;

row(ss)=matrix(ii,jj);

    while ss<=35

        ss=ss+1;

        jj=jj+1;

        row(ss)=matrix(ii,jj);

        x=ii;

        y=jj;

        while (ii~=y & jj~=x) & ss<=36 

            ii=ii+1;

            jj=jj-1;

            ss=ss+1;

            row(ss)=matrix(ii,jj);

        end

        if ss<=35

            ss=ss+1;

            ii=ii+1;

            row(ss)=matrix(ii,jj);

            x=ii;

            y=jj;

        end

        while (ii~=y & jj~=x) & ss<=35

            ii=ii-1;

            jj=jj+1;

            ss=ss+1;

            row(ss)=matrix(ii,jj);

        end

    end

 % second part   

    while ss < 64

          ss=ss+1;

          jj=jj+1;

          row(ss)=matrix(ii,jj);

          x=ii;

          y=jj;

        while (ii~=y & jj~=x) & ss<64 

            ii=ii-1;

            jj=jj+1;

            ss=ss+1;

            row(ss)=matrix(ii,jj);

        end

        if ss<=63

            ss=ss+1;

            ii=ii+1;

            row(ss)=matrix(ii,jj);

            x=ii;

            y=jj;

        end

        while (ii~=y & jj~=x) & ss<=64

            ii=ii+1;

            jj=jj-1;

            ss=ss+1;

            row(ss)=matrix(ii,jj);

        end

    end

عملیات ماتریسی MATLAB از قواعد جبرخطی پیروی می کند .
A+B عبارت است از جمع دو بردار یا ماتریس A و  B . دو داده A و B باید هم اندازه باشند . البته یکی از آنها می تواند اسکالر نیز باشد . عدد اسکالر می تواند با هر ماتریس و یا آرایه ای جمع شود .

A-B عبارت است از تفریق دو بردار و یا ماتریس A و B . دو داده A و B باید هم اندازه باشند . البته یکی از آنها می تواند اسکالر نیز باشد . عدد اسکالر می تواند از هر ماتریس و یا آرایه ای کم شود .

A*B عبارت است از ضرب ماتریسی دو ماتریس A و B . اندازه A و B باید از قانون ضرب ماتریس ها تبعیت کند . البته یکی از آنها می تواند اسکالر نیز باشد .

A’ عبارت است از ترانهاده ماتریس A که با تعویض سطرها و ستونها حاصل می شود .

>> A=[1 2 3;4 5 6;7 8 9]

A =

1     2     3
4     5     6
7     8     9

>> A'

ans =

1     4     7
2     5     8
3     6     9

دستگاه فوق را می توان به فرم زیر نیز نوشت :

برای حل اینگونه معادلات هیچ محدودیتی وجود ندارد البته در حالت کلی اگر دترمینان ماتریس A صفر باشد دستگاه جواب ندارد . در زیر برنامه حل مثالی که در بالا بیان گردید مشاهده می شود .

فرم کلی یک چندجمله ای به صورت

می باشد که در MATLAB با بردار سطری [a₀ a₁... a_n-2 a_n-1 a_n] نمایش داده می شود .

مثال) نمایش چندجمله ای f(x)=3x⁴-0.5x³+x-5.2 در MATLAB به صورت زیر می باشد :

برای محاسبه مقدار چندجمله ای در یک نقطه خاص از دستور polyval استفاده می شود .

مثال) مقدار چمدجمله ای فوق را در نقطه x=1 پیدا کنید .

برای پیدا کردن ریشه ها از دستور roots استفاده می شود .

مثال) ریشه های چندجمله ای فوق را پیدا کنید .

برای ضرب دو چندجمله ای در یکدیگر از تابع conv استفاده می شود .

مثال) برای ضرب دو چندجمله ای f(x)=3x³-5x²+6x-2 و g(x)=x⁵+3x⁴-x²+2.5 به صورت زیر عمل می شود .

MATLAB تابع مستقیمی برای جمع دو چندجمله ای ندارد .

اگر بردارهای دوچندجمله ای هم اندازه باشند ، می توان از جمع استاندارد برداری استفاده کرد . اگر بردارهای دوچندجمله ای هم اندازه نباشند ، بایستی به بردار کوچکتر به اندازه کافی صفر اضافه شود تا هر دو بردار هم اندازه شوند .

برای مشتق گیری و انتگرال گیری از یک چند جمله ای به ترتیب از توابع polyder و polyint استفاده می شود .

مثال) مشتق تابع (x³+x-1)(x+4)(3x²+6x+9) را بدست آورید .

دستور plot

برای رسم نمودارها و منحنی ها در MATLAB از دستور plot استفاده می شود . این دستور یک پنجره گرافیکی موسوم به figure window ایجاد می کند و باعث ترسیم شکل برروی پنجره figure ایجاد شده می گردد . دستور plot(x,y) بردار y را بر حسب x رسم می کند .

مثال 1)

مثال2) اضافه کردن برچسب به محورهای مختصات با استفاده از دستورات xlabel و ylabel انجام می شود .

مثال3) با دستور title می توان یک خط متن در بالای شکل نوشت .

مثال4 ) با دستور text می توان یک عبارت متنی را در هر نقطه از شکل نوشت . فرم کلی این دستور به صورت

می باشد که در این رابطه (x,y) مختصات مرکز لبه سمت چپ عبارت متنی بر حسب واحدهای موجود بر روی محور شکل است .

مثال5) با دستور axis می توان مقادیر حداقل و حداکثر محورهای مختصات را تنظیم نمود . فرم کلی تابع در این حالت به صورت

می باشد .

مثال6) با دستور axis auto مقادیر حداقل و حداکثر محورهای مختصات به طور خودکار تنظیم می شود .

مثال7) می توان نوع خطوط منحنی را با دستور plot تعیین نمود . بطور مثال می توان خط را توپر ، نقطه چین و ... انتخاب نمود .

هرچند که MATLAB یک نرم افزار مخصوص مسایل آنالیز عددی می باشد ولی قادر است مسایل مربوط به معادلات دیفرانسیل را به طور نمادین حل نماید . به عنوان مثال می خواهیم معادله دیفرانسیل زیر را حل کنیم .

تابع مورد استفاده در این مبحث ، dsolve می باشد که مخصوص حل نمادین معادلات است . مثال مطرح شده را این گونه حل می کنیم :

حل معادلات با شرایط مرزی :

کافی است شرایط مرزی را در تابع dsolve وارد نماییم .

برای آشنایی بیشتر به حل مثال دیگری می پردازیم :

بعد از حل معادله ، برای نمایش بهتر y ، می توان دستور pretty را اجرا نمود .

در این حالت نیز همانند معادلات مرتبه اول از تابع dsolve استفاده می کنیم . به عنوان مثال ، معادله زیر را به کمک MATLAB حل می کنیم .

حل معادلات با شرایط مرزی :

کافی است شرایط مرزی را در تابع dsolve وارد نماییم .

حال تابع را رسم می کنیم :

در این حالت نیز همانند معادلات مرتبه اول و دوم از تابع dsolve استفاده می کنیم . به عنوان مثال ، معادله زیر را به کمک MATLAB حل می کنیم .

پس مشاهده می شود که این تابع در MATLAB تعریف شده می باشد و به صورت زیر می باشد :

و P_n تابع چندجمله ای لژاندر از مرتبه n می باشد و به صورت زیر تعریف می شود :

در این حالت تابع مورد نظر را بر حسب t وارد می کنیم و آن را در ورودی دستور laplace قرار می دهیم . خروجی دستور بر حسب s می باشد :

برای درک بهتر خروجی ، می توانید دستور pretty را بکار برید . حال به ارائه مثال دیگری از تبدیل لاپلاس می پردازیم .

در این حالت تابع مورد نظر را بر حسب s وارد می کنیم و آن را در ورودی دستور ilaplace قرار می دهیم . خروجی دستور بر حسب t می باشد .

تابع B(s)/A(s)  زیر را در نظر بگیرید .

که در آن ، بعضی a_i ها و b_i ها ممکن است صفر باشد . در MATLAB ضرایب چندجمله ایهای صورت و مخرج در بردارهای ردیفی مشخص می شوند . یعنی :

دستور

باقیمانده ها (r)  ، قطبها (p)  و جملات غیرکسری (k)  نسبت دو چندجمله ای B(s)  و A(s) را بدست می دهد . بسط به کسرهای جزئی B(s)/A(s) عبارت است از :

مثال ) تابع تبدیل زیر را در نظر بگیرید :

برای این تابع

با اجرای دستور معرفی شده ، خواهیم داشت :

توجه کنید که باقیمانده ها در بردار ستونی r ، محل قطبها در بردار ستونی p  و خارج قسمت در بردار ردیفی k  برگردانده می شود . یعنی بسط کسرهای جزئی B(s)/A(s)   بدست آمده با MATLAB  عبارت است از :

در MATLAB برای یافتن صفرها ، قطبها و بهره k  تابع B(s)/A(s)  می توان دستور زیر را بکار برد :

سیستم تعریف شده به صورت زیر را در نظر بگیرید :

برای یافتن صفرها (z) ، قطبها (p) و بهره (k) دستورات زیر را وارد می کنیم :

در اینصورت ، کامپیوتر خروجی زیر را بدست می دهد :

اجازه دهید تابع تبدیل حلقه بسته را به صورت زیر بنویسیم :

پس از تبدیل این تابع تبدیل ، دستور زیر نمایش فضای حالت را بدست می دهد :

توجه به این نکته مهم است که نمایش فضای حالت سیستمها ، نمایش یکتا نیست . برای هر سیستمی تعداد زیادی (بی نهایت) نمایش فضای حالت وجود دارد . دستور MATLAB یکی از این نمایشهای فضای حالت را به دست می دهد .

برای یافتن تابع تبدیل از معادلات فضای حالت ، دستور زیر را بکار می بریم :

همانطور که می دانید سیستم مرتبه دوم

سیستم مرتبه دوم استاندارد نامیده می شود . با داشتنω_n و ξ ، دستور

چندجمله ای صورت و مخرج سیستم مرتبه دوم زیر را بدست می دهد :

پس اگر برای مثال داشته باشیم =5 rad/s  ω_n و =0.4  ξ می توانیم با استفاده از کدهای زیر ، سیستم مرتبه دوم متناظر با آن را بدست آوریم .

اگر num و den (صورت و مخرج تابع تبدیل حلقه بسته) معلوم باشد دستورهایی مانند :

منحنی پاسخ پله سیستم را ایجاد می کنند . (در دستور دوم t زمانهای تعیین شده توسط کاربر را در بر دارد .)

مثال) پاسخ پله سیستمی با تابع تبدیل حلقه بسته زیر را ترسیم نمایید .

پس از اجرای کدهای فوق ، خواهیم داشت :

سیستم با تابع تبدیل حلقه بسته زیر را در نظر بگیرید .

منحنی پاسخ پله c(t) را به ازای ξ های مختلف رسم کنید .

برای رسم منحنی پاسخ پله این سیستم کنترلی ، یک m-file ایجاد کرده و کدهای زیر را درون آن وارد می کنیم .

و پس از اجرا ، خواهیم داشت :

در MATLAB ، دستور ramp برای یافتن پاسخ شیب وجود ندارد . بنابراین باید برای یافتن پاسخ شیب ، از دستور step استفاده کنیم . دقیقتر اینکه برای یافتن پاسخ شیب سیستمی با تابع تبدیل G(s) ، G(s) را بر s تقسیم می کنیم و دستور پاسخ پله را بکار می بریم . برای مثال سیستم حلقه بشته ای با تابع تبدیل زیر را در نظر بگیرید .

برای ورودی شیب واحد ، R(s)=1/s² . پس

برای یافتن پاسخ شیب این سیستم ، صورت و مخرج زیر را به MATLAB داده و دستور پاسخ پله را بکار می بریم .

برنامه MATLAB به صورت زیر است .

منحنی زیر ، خروجی برنامه را نشان می دهد .

برای یافتن پاسخ به ازای ورودی دلخواه می توان دستور Isim را به کار برد . دستور زیر پاسخ به ورودی زمانی r بدست می دهند .

مثال ) سیستمی با تابع تبدیل حلقه بسته زیر را در نظر بگیرید .

پاسخ این سیستم به ورودی R = e^-t را رسم کنید .
در محیط MATLAB ، یک m-file ایجاد کرده و کدهای زیر را در آن وارد می کنیم .

پس از اجرا ، خروجی برنامه به صورت زیر خواهد بود .

اگر بخواهیم خطوطی با ξ مشخص ( مثلا خط ξ=0.5 و خط ξ=0.707 ) و دایره های ω_n ثابت خاصی ( مثلا دایره ω_n=1 و خط ω_n=2 ) رسم شود باید دستور زیر را بکار بریم

را بکار ببریم . برای این منظور ابتدا در محیط MATLAB یک m-file ساخته و کدهای زیر را در آن وارد کنید .

پس از اجرا ، خروجی به صورت زیر خواهد بود .