Introduction

The NACA 0012 airfoil is widely used. The simple geometry and the large amount of wind tunnel data provide an excellent 2D validation case. For this case I use the Spalart-Allmaras turbulence model.

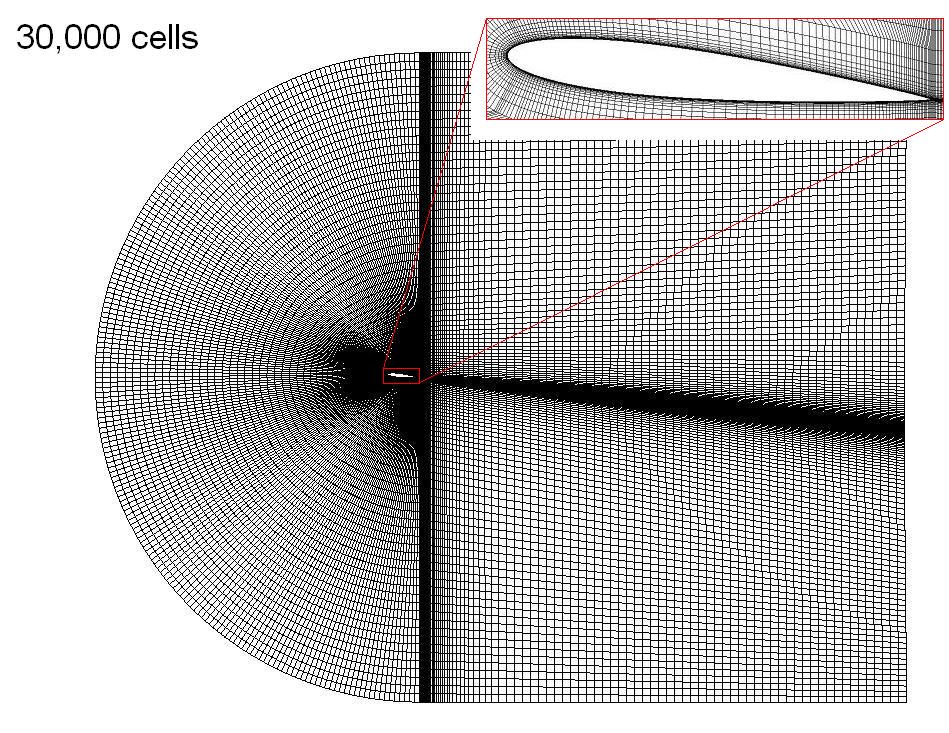
Mesh

The mesh is a 30,000 cell structured C-grid. The chord length is 1 m. The width of the first cell at the airfoil boundary is 0.02 mm. At Re = 3e6 and zero angle of attack, this results in a wall y+ = 1.3 ± 0.4, which is low enough for the turbulence model to resolve the sub layer. The mesh shown is for an angle of attack of 6 degrees.

Drag Coefficient

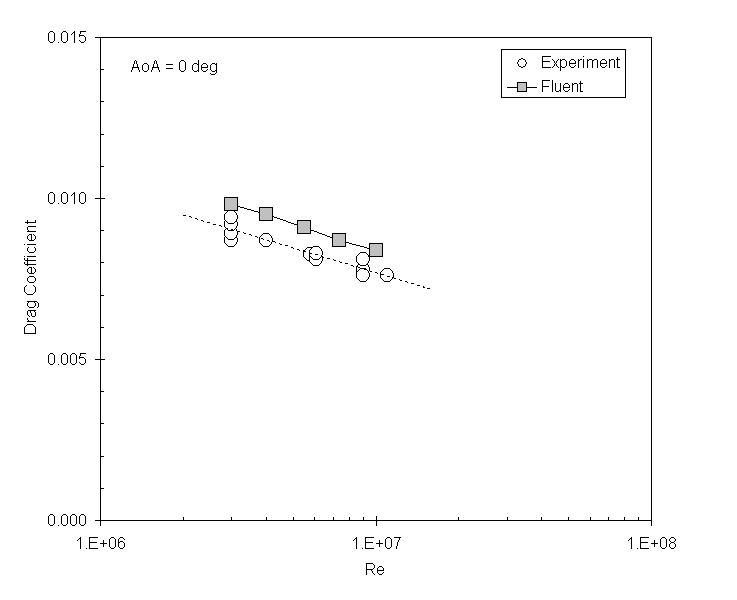
The drag coefficient at zero angle of attack depends on the Reynold's number. The experimental data is for an airfoil with a trip wire, which forces the boundary layer to be completely turbulent.[1] This corresponds to the Fluent model, which has an active turbulence model over the complete airfoil. Note that the calculated drag coefficient is somewhat higher than the experimental one. Possibly, the modeled boundary layer is turbulent from the beginning, while in reality the trip wire is not at the very leading edge of the foil.

Modeling the NACA 0012 airfoil without a trip wire is more complicated, since Fluent itself is unable to predict the point along the chord where the transition from a laminar to a turbulent boundary layer takes place. One option is to manually set this transition point at Re = 5e5, which is the flat plate transition point.[2]

Lift Curve

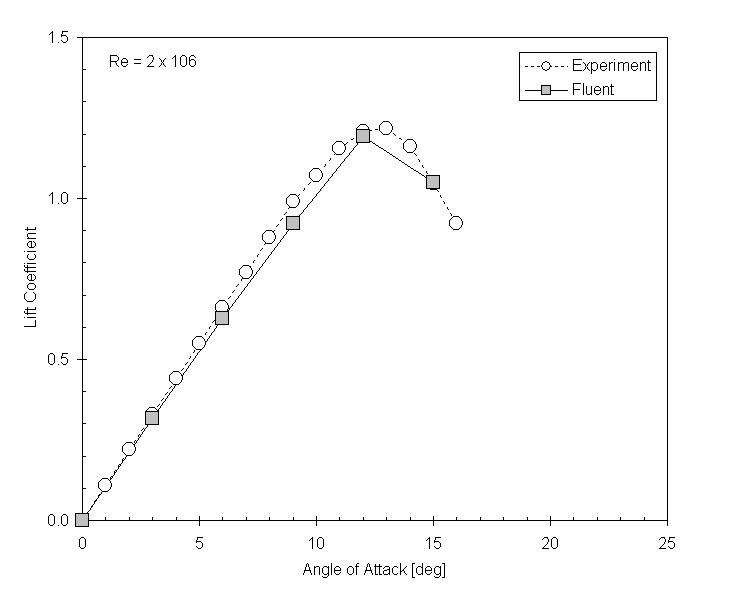
The lift coefficient depends on the angle of attack. For Re = 2e6 I compare the lift coefficient to experimental results.[3] Because the lift coefficient is less sensitive to the transition point, the experimental data is for an airfoil without trip wire. (Later note: I have come to think that the presence of a stall angle has some element of luck. It turns out to be quite difficult to get one in Fluent.)

Lift Curve Slope

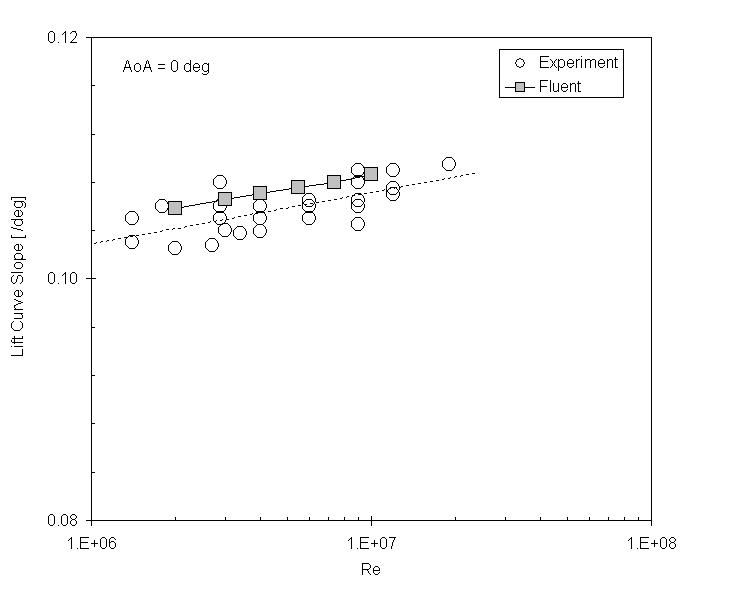
The initial slope of the lift curve depends on the Reynold's number. Here I compare the lift curve slope to experimental results.[1] Experimental results are both with and without trip wire; again the lift coefficient is less sensetive to the transition point than the drag coefficient.

References