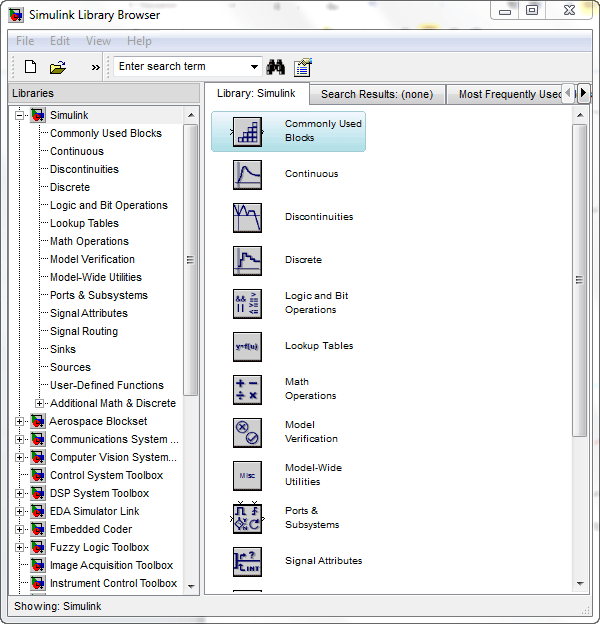
از منوی File ، گزینه New و سپس گزینه Model را انتخاب کنید . یک پنجره خالی به شکل زیر باز می شود :
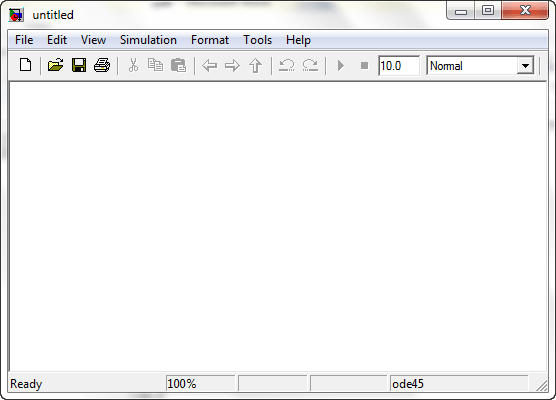
این پنجره را پنجره Model می نامیم . آنچه که از این به بعد باید انجام دهیم این است که بلوک هایی (blocks) را که می خواهیم از library های سیمولینک انتخاب کنیم و آنها را در پنجره Model کپی کنیم .
در ادامه مثال مطرح شده در بخش سیمولینک کتاب زیر را برای شما شرح خواهم داد :
A Guide to MATLAB for Beginners and and Experienced Users
فرض کنید بخواهیم معادله دیفرانسیل
 را در سیمولینک نرم افزار متلب مدل سازی کنیم . چون متغیر زمان به صورت
پیوسته می باشد بنابراین از پنجره Simulink Library Browser ، گزینه
Continuous را انتخاب می کنیم . بلوک های library Continuous به صورت شکل
زیر نمایش داده می شوند :
را در سیمولینک نرم افزار متلب مدل سازی کنیم . چون متغیر زمان به صورت
پیوسته می باشد بنابراین از پنجره Simulink Library Browser ، گزینه
Continuous را انتخاب می کنیم . بلوک های library Continuous به صورت شکل
زیر نمایش داده می شوند :
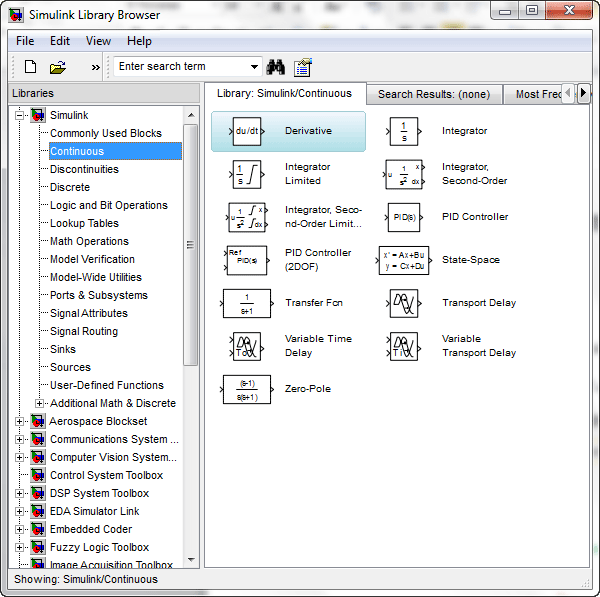
برای انتخاب بلوک های مورد نظرمان باید دقت داشته باشیم که u را می توانیم با انتگرال گیری از 'u به دست آوریم و 'u را می توانیم با انتگرال گیری از ''u به دست آوریم . بنابراین به دو بلوک انتگرال گیر نیاز داریم . برای قرار دادن بلوک انتگرال گیر در پنجره Model ، ابتدا در پنجره Simulink Library Browser بر روی بلوک انتگرال گیر (integrator) با موس کلیک کنید (کلیک سمت چپ) و بدون رها کردن کلید موس ، موس را بر روی محلی در پنجره model ببرید و سپس کلید موس را رها کنید . یک بلوک انتگرال گیر در پنجره Model نمایش داده خواهد شد . به همین روش یک بلوک انتگرال گیر دیگر را در پنجره model رسم کنید . بنابراین شکل زیر را خواهیم داشت :
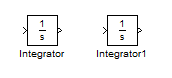
حال برای آنکه دو بلوک را به یکدیگر رسم کنیم باید ابتدا بر روی خروجی بلوک اول با موس کلیک کنیم (کلیک سمت چپ) و بدون رها کردن کلید موس ، موس را بر روی ورودی بلوک دوم ببریم و سپس کلید موس را رها کنیم . یک فلش بین دو بلوک رسم خواهد شد که نشان دهنده اتصال دو بلوک به یکدیگر می باشد . البته برای اتصال دو بلوک به یکدیگر روش دیگری نیز وجود دارد و آن این است که ابتدا بلوک منبع (source block) را با موس انتخاب کنیم و سپس کلید Ctrl از کیبورد را پایین نگه داریم و سپس بر روی بلوک مقصد (destination block) با موس کلیک کنیم (کلیک سمت چپ) . شکل بلوک ها به صورت زیر خواهد بود :
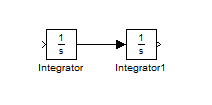
همچنین اگر دقت کنید نام هر بلوک در زیر آن نوشته شده است ، می توانیم بر روی نام هر بلوک کلیک کنیم و نام آن را تغییر بدهیم . بنابراین نام هر بلوک را به صورت شکل زیر تغییر می دهیم :
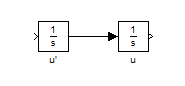
معادله دیفرانسیل را می توانیم به صورت
 بازنویسی کنیم . بنابراین به 3 بلوک بهره (Gain) و یک بلوک جمع (Sum) نیاز
داریم که آنها را می توانیم در Math Operations Library بیابیم . با ترسیم
آنها ، شکل بلوک ها به صورت زیر در می آید :
بازنویسی کنیم . بنابراین به 3 بلوک بهره (Gain) و یک بلوک جمع (Sum) نیاز
داریم که آنها را می توانیم در Math Operations Library بیابیم . با ترسیم
آنها ، شکل بلوک ها به صورت زیر در می آید :
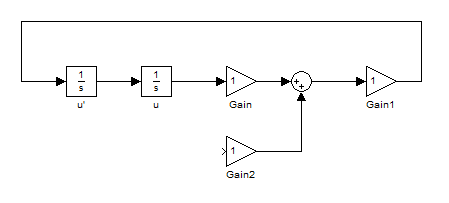
اما اگر در شکل بالا دقت کنید ، متوجه می شوید که میزان بهره بلوک های بهره برابر 1 می باشد و مقدار بهره آنها را باید تغییر بدهیم . برای این منظور باید بر روی هر کدام از بلوک های بهره دو بار کلیک (دابل کلیک) کنیم تا پنجره Function Block Parameters باز شود . این پنجره به شکل زیر می باشد :
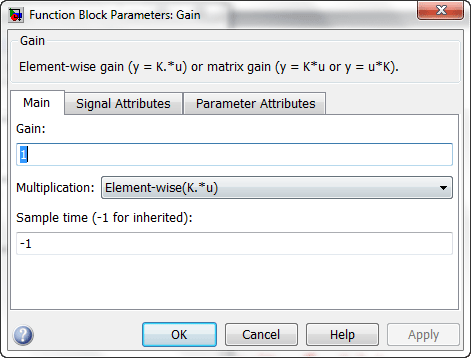
در این پنجره مقدار بهره مورد نظر خود را باید در قسمت Gain بنویسید . بنابراین مقدار بهره بلوک Gain را برابر 5 ، مقدار بهره بلوک Gain1 را برابر 1- و مقدار بهره بلوک Gain2 را برابر 2 قرار می دهیم . مشاهده خواهید کرد که مقدار بهره ها درون هر بلوک نمایش داده می شود :
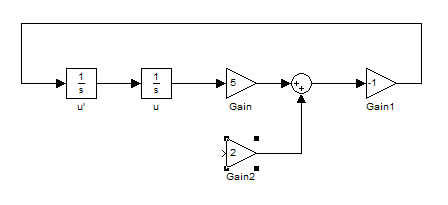
حال باید خروجی بلوک انتگرال گیر 'u را به ورودی بلوک Gain2 متصل کنیم اما چون بلوک انتگرال گیر تنها یک خروجی دارد باید یک انشعاب از خروجی بلوک انتگرال گیر بگیریم . برای این منظور موس را بر روی وسط فلشی که دو بلوک انتگرال گیر را به هم متصل کرده است می بریم و سپس کلید Ctrl از کیبورد را فشار داده و پایین نگه می داریم آنگاه با موس کلیک می کنیم (کلیک سمت چپ) و همان طور که کلید موس را نگه داشته ایم نشانگر موس را بر روی ورودی بلوک Gain2 می بریم و آنگاه کلید موس را رها می کنیم . یک فلش در بین بلوک انتگرال گیر و بلوک Gain2 ساخته خواهد شد . شکل بلوک ها به صورت زیر در می آید :
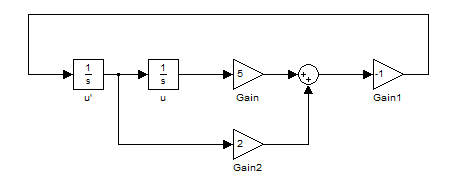
بلوک های لازم برای مدل سازی معادله دیفرانسیل را در پنجره Model قرار دادیم اما اکنون به بلوکی نیاز داریم تا خروجی را با آن مشاهده کنیم . برای این منظور از Sinks Library بلوک Scope را انتخاب کرده و آن را در پنجره مدل قرار می دهیم :
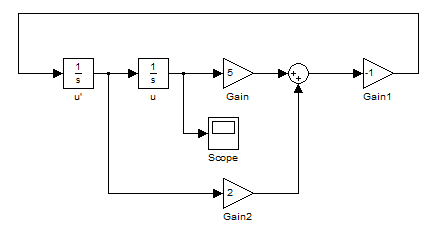
دقت داشته باشید که اگر بلوکی را اضافه کردید و مشاهده کردید که ساختار شکلتان زیادی فشرده است و بلوک جدید در جای مناسبی قرار نگرفته است ، می توانید هر بلوک دلخواه را با موس جابجا کنید تا در محل مناسبتری قرار بگیرد .
اکنون زیرنویس بلوک های مختلف را تغییر می دهیم تا نقش هر بخش مدل به طور دقیق مشخص باشد . چنانچه تمایل داشته باشید عبارتی را در زیر یک فلش بنویسید تنها کافی است که بر روی آن فلش با موس دو بار کلیک (دابل کلیک) کنید و کادری نمایش داده خواهد شد که در ان می توانید عبارت مورد نظر خود را بنویسید .
شکل نهایی بلوک ها به صورت زیر می شود :
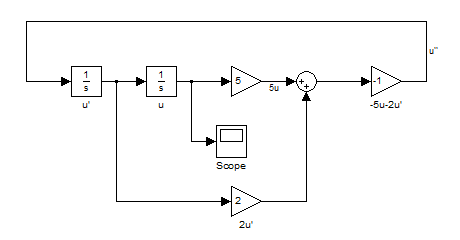
حال برای مشاهده نتیجه ابتدا باید مدل ساخته شده را Save کنیم . از منوی File گزینه Save را انتخاب کنید و سپس با نامی دلخواه مدل ساخته شده را در محل مورد نظرتان Save کنید .
ممکن است بخواهیم برای معادله دیفرانسیل ، شرایط اولیه تعریف کنیم . مثلا فرض کنید شرایط اولیه زیر را برای معادله دیفرانسیل داشته باشیم :

که با این شرایط اولیه ، پاسخ معادله دیفرانسیل به صورت زیر خواهد بود :

برای اعمال شرایط اولیه ذکر شده ابتدا بر روی بلوک انتگرال گیر اول که مربوط به u' می باشد ، با موس دو بار کلیک (دابل کلیک) کنید و سپس در پنجره ای که باز می شود مقدار نوشته شده در زیر Initial condition را به مقدار 5 تغییر بدهید . سپس بر روی بلوک انتگرال گیر دوم که مربوط به u می باشد ، با موس دو بار کلیک (دابل کلیک) کنید و سپس در پنجره ای که باز می شود مقدار نوشته شده در زیر Initial condition را به مقدار 1 تغییر بدهید .
برای آنکه بتوانید مشاهده کنید که در حین شبیه سازی چه اتفاقاتی می افتد باید قبل از شبیه سازی بر روی بلوک Scope با موس دو بار کلیک کنید تا پنجره نمایش آن باز شود . در این پنجره پس از شبیه سازی ، مقدار u به صورت تابعی از t رسم خواهد شد . این پنجره به شکل زیر می باشد :
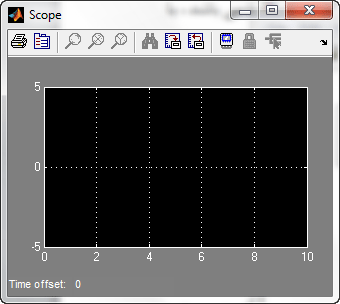
حال برای مشاهده شبیه سازی از منوی Simulation گزینه Start را انتخاب کنید . شبیه سازی انجام می شود و مقدار u به صورت تابعی از t به صورت شکل زیر نمایش داده می شود :
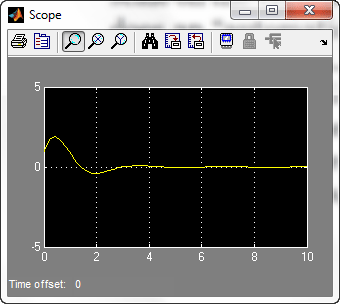
این شکل نمایش پاسخ معادله دیفرانسیل با شرایط اولیه ذکر شده می باشد . در پنجره Scope بر روی گزینه Autoscale کلیک کنید تا مقادیر پاسخ در شکل به طور دقیق نمایش داده شود :
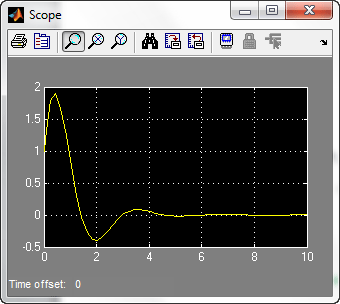
برچسبها: کد متلب الگوریتم سیمپلکس, متلب سایت, دانلود کد رایگان الگوریتم ازدحام ذرات, PSO

فرض کنید قرار است محیط بسته ای که دو معادله ی زیر با هم می سازند با رنگ سبز (بدون منظور خاصی !) پر کنیم :
y=x+1
y=x^2
بسیاری از کاربران متلب خیلی ساده می دانند که برای پر کردن محیط بسته با رنگ خاص در متلب می توان از فرمان fill استفاده کرد اما روش درست استفاده از آن کمی پیچیده است
ابتدا دستور hold را فعال کرده و دو نمودار را رسم می کنیم :
hold on;
ezplot('x+1');
ezplot('x^2');
برای رسم دقیق قسمت پر کننده شما نیاز به دانستن محل تقاطع دو خط دارید و برای این کار هم لازم است معادله ی آن دو با هم حل شود :
s=solve('y=x+1','y=x^2');
شکل کلی فرمان fill به صور ت زیر است
fill(X,Y,ColorSpec)
که در آن x و y مجموعه ی نقاطی هستند که یک محیط بسته ی دو بعدی را تشکیل می دهند و نیز رنگ زمینه را هم در قسمت آخر همانند دستور plot تعیین می کنید
باقی کار چندان مشکل نیست فقط شما نیاز دارید که x ها در بین دو نقطه ی تقاطع منحنی جای بگیرند و y ها هم از روی یکی از معادلات به طور دقیق محاسبه شوند، هر چه تعداد نقاط بیشتر باشد هاشور دقیقتر شکل می گیرد
f2=x^2;
x=linspace(subs(s.x(1)),subs(s.x(2)),3);
y2=subs(f2,x);
fill(x,y2,'g');
plot(x,y2,'r+')
axis([-2 2 -1 4])
برای درنظر گرفتن تعداد نقاط بیشتر می توانید در فرمان linspace بجای عدد 3 از 30 یا 40 استفاده کنید و ببینید تغییرات به چه صورت خواهد بود.
متن کامل برنامه به صورت زیر است :
|
clc; hold on; ezplot('x+1'); ezplot('x^2'); s=solve('y=x+1','y=x^2'); syms x; f2=x^2; x=linspace(subs(s.x(1)),subs(s.x(2)),3); y2=subs(f2,x); fill(x,y2,'g'); plot(x,y2,'r+') axis([-2 2 -1 4]) |
برچسبها: متلب, دانلود کتاب آموزش نرم افزار MATLAB, اموزش جامع نرم افزار متلب, دانلود برنامه نويسي Matlab
از دوستانی که قبلا این فایلهارا درنت قرار داده بودند دوباره تشکر میکنیم
دانلود فایل اموزشی سیمولینک متلب
دانلود
پسورد : spow
برچسبها: دانلود کتاب آموزش نرم افزار MATLAB, اموزش جامع نرم افزار متلب, دانلود برنامه نويسي Matlab, کد متلب الگوریتم سیمپلکس

http://www.mediafire.com/?nx4ss2z9e0h4xb1
برچسبها: کد متلب الگوریتم سیمپلکس, متلب سایت, دانلود کد رایگان الگوریتم ازدحام ذرات, PSO
